L'hypothèse de Riemann en dessin
L’hypothèse de Riemann est une conjecture formulée par Riemann en 1859, dans l’unique travail qu’il a consacré à la théorie des nombres. Elle porte sur les points d’annulation de la fonction $\zeta$ et a pour conséquence de pouvoir estimer avec un bon terme d’erreur le nombre de nombres premiers inférieurs à une valeur donnée.
Notons $\mathcal{P}$ l’ensemble infini des nombres premiers. Pour tout réel $t\geq 2$, on note $\pi(t)$ le nombre de nombres premiers inférieurs à $t$, autrement dit $\pi(t)=\#\{p\in\mathcal{P}\colon p\leq t\}.$ Si $\mathrm{Li}(t)=\int_2^t\frac{dx}{\ln(x)}$ (savoir ce que c’est n’est pas tout à fait nécessaire à la compréhension de la suite, retenez que c’est un nombre que les mathématiciennes et mathématiciens savent calculer pour chaque valeur de $t$, par exemple $\mathrm{Li}(10)=5,12…$ et $\mathrm{Li}(1000000000000)=37607950279,75970$…, précisément, c’est la surface déterminée par la courbe d’équation $y=\frac{1}{\log(x)}$ et les trois droites $x=2$, $x=t$ et $y=0$), Gauss a conjecturé que $\mathrm{Li}(t)$ est une bonne approximation de $\pi(t)$. Cela signifie que le nombre de nombres premiers inférieurs à $t$ (qui est difficile à calculer si $t$ est très grand) peut être évaluer, avec une erreur que l’on espère faible, en calculant $\mathrm{Li}(t)$, nombre plus facile à calculer. Le tableau suivant permet de tester cette conjecture.
| $t$ | $\pi(t)$ | $\mathrm{Li}(t)$ | $\pi(t)-\mathrm{Li}(t)$ | Erreur (%) |
|---|---|---|---|---|
| 10 | 4 | 5,12 | 1,12 | 28,0 |
| 100 | 25 | 29,08 | 4,08 | 16,3 |
| 1000 | 168 | 176,56 | 8,56 | 5,10 |
| 10000 | 1229 | 1245,09 | 16.09 | 1,31 |
| 100000 | 9592 | 9628,76 | 36,76 | 0,38 |
| 1000000 | 78498 | 78626,50 | 128,50 | 0.16 |
| 10000000 | 664579 | 664917,36 | 338,36 | 0,05 |
| 100000000 | 5761455 | 5762208,33 | 753,33 | 0,01 |
| 1000000000 | 50847534 | 50849233,91 | 1699,91 | 0,003 |
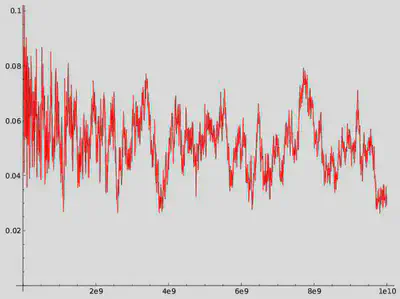
Hadamard et de la Vallée-Poussin sont les premiers, en 1896, à avoir quantifié l’erreur en montrant qu’elle ne pouvait pas être trop grande. Plus précisément, ils ont démontré qu’il existe des réels $C$ et $a>0$ tels que, pour tout réel $t\geq 2$ on a $$\left|\pi(t)-\mathrm{Li}(t)\right|\leq Ct\mathrm{e}^{-a\sqrt{\ln(t)}}.$$ C’est le théorème des nombres premiers. Ce n’est pas le meilleur résultat possible : on conjecture que l’erreur est bien plus petite que ce qu’indiqué par Hadamard et de la Vallée Poussin. On conjecture que le meilleur résultat possible est le suivant : il existe un réel $C$ tel que, pour tout réel $t\geq 2$ on a $$\left|\pi(t)-\mathrm{Li}(t)\right|\leq C\sqrt{t}\ln(t).$$ Cette inégalité est équivalente à l’hypothèse de Riemann. La figure ci-dessous représente le graphe de la fonction $$ t\mapsto\frac{\left|\pi(t)-\mathrm{Li}(t)\right|}{\sqrt{t}}. $$ La conjecture indique que le graphe de cette fonction ne devrait pas prendre de trop grandes valeurs. Pour se rendre compte de la qualité de l’approximation, on comparera l’échelle verticale et l’échelle horizontale.
Pour tout entier naturel $n\geq 1$, on peut évaluer la somme $$ \sum_{k=1}^n\frac{1}{k^2}=1+\frac{1}{2^2}+\frac{1}{3^2}+\dotsm+\frac{1}{n^2}. $$ On note $S(n)$ cette somme. Le tableau suivant donne quelques valeurs de $S(n)$.
| $n$ | $S(n)$ |
|---|---|
| 1 | 1 |
| 10 | 1,5498 |
| 100 | 1,6350 |
| 1000 | 1,6439 |
| 10000 | 1,6448 |
| 100000 | 1,6449 |
| 1000000 | 1,6449 |
Il semble que $n$ grandissant, la valeur de $\sum_{k=1}^n\frac{1}{k^2}$ se rapproche d’une valeur dont le développement décimal commence par $1,644$. On peut montrer que ce phénomène persiste si $n$ prend des valeurs de plus en plus grandes : plus grand est $n$, plus $S(n)$ se rapproche d’une valeur. On dit que la somme converge et on note $\sum_{k=1}^{+\infty}\frac{1}{k^2}$ le nombre réel approché. On a calculé la somme des inverses des carrés. Nous aurions pu calculer la somme des inverses des cubes : $\sum_{k=1}^n\frac{1}{k^3}$. De nouveau la tableau suivant suggère que $n$ grandissant, la valeur de $\sum_{k=1}^n\frac{1}{k^3}$ se rapproche d’une valeur dont le développement décimal commence par $1,202$. Le tableau suivant donne quelques valeurs de $T(n)=1+\frac{1}{2^3}+\frac{1}{3^3}+\dotsm+\frac{1}{n^3}$.
| $n$ | $T(n)$ |
|---|---|
| 1 | 1 |
| 10 | 1,1975 |
| 100 | 1,2020 |
| 1000 | 1,2021 |
| 10000 | 1,2021 |
| 100000 | 1,2021 |
| 1000000 | 1,2021 |
on note $\sum_{k=1}^{+\infty}\frac{1}{k^3}$ le nombre réel approché. On peut montrer que ce qu’on vient de dire pour $2$ et $3$ peut être fait pour n’importe quel entier naturel au moins égal à $2$. Pour tout entier $m\geq 2$, on note $$\zeta(m)=\sum_{k=1}^{+\infty}\frac{1}{k^m}=1+\frac{1}{2^m}+\frac{1}{3^m}+\frac{1}{4^m}+\dotsm.$$ En revanche, on ne peut pas le faire pour $n=1$ comme le suggère le tableau ci-dessous qui donne quelques valeurs de $U(n)=1+\frac{1}{2}+\frac{1}{3}+\dotsm+\frac{1}{n}$.
| $n$ | $U(n)$ |
|---|---|
| 1 | 1 |
| 10 | 2,9290 |
| 100 | 5,1874 |
| 1000 | 7,4855 |
| 10000 | 9,7876 |
| 100000 | 12,090 |
| 1000000 | 14,393 |
On ne peut pas non plus le faire pour $n=0$ ; en effet, $$1+\frac{1}{2^0}+\frac{1}{3^0}+\dotsm+\frac{1}{n^0}$$ est une somme de $1$ répétés $n$ fois, elle vaut $n$ et est donc de plus en plus grande). Si $n^2$ a un sens bien connu (c’est le produit de $n$ par $n$), en revanche $n^{5,2}$ ne semble pas avoir de sens. Les mathématiciennes et mathématiciens savent donner un sens à ce nombre. Votre calculatrice vous dira par exemple que le développement décimal de $3^{5,2}$ commence par $302,7126$. On sait alors montrer que, quelque soit la valeur du nombre réel $x>1$, la somme $$1+\frac{1}{2^x}+\frac{1}{3^x}+\dotsm+\frac{1}{n^x}$$ s’approche, $n$ grandissant, d’un nombre réel que l’on note $\zeta(x)$. Par exemple, le développement décimal de $\zeta(5,2)$ commence par $1,031$. le tableau ci-dessous qui donne quelques valeurs de $$V(n)=1+\frac{1}{2^{5,2}}+\frac{1}{3^{5,2}}+\dotsm+\frac{1}{n^{5,2}}.$$
| $n$ | $V(n)$ |
|---|---|
| 1 | 1 |
| 10 | 1,0316 |
| 100 | 1,0317 |
| 1000 | 1,0317 |
| 10000 | 1,0317 |
| 100000 | 1,0317 |
| 1000000 | 1,0317 |
L’histoire ne s’arrête pas là… Au lieu de considérer un nombre réel, on peut considérer des couples de nombres réels sur lesquels on sait faire des opérations (cela s’appelle les nombres complexes). Si $x$ et $t$ sont deux nombres réels, on considère le couple $(x;t)$ et on sait calculer $n^{(x;t)}$ pour tout entier $n\geq 1$. Par exemple une calculatrice scientifique devrait vous dire que $3^{(5,2;-7,3)}$ est un couple de réels dont les développements décimaux commencent par $(-49,9864;-298,5570)$. On sait alors montrer que, quelque soit le couple de nombres réels $(x;t)$, la somme $$ \sum_{k=1}^n\frac{1}{k^{(x;t)}}=1+\frac{1}{2^{(x;t)}}+\frac{1}{3^{(x;t)}}+\dotsm+\frac{1}{n^{(x;t)}}. $$ s’approche, $n$ grandissant, et à condition que $x>1$ d’un nombre réel que l’on note $\zeta(x;t)$. Le tableau suivant donne quelques valeurs de $$ W(n)=1+\frac{1}{2^{(5,2;-7,3)}}+\frac{1}{3^{(5,2;-7,3)}}+\dotsm+\frac{1}{n^{(5,2;-7,3)}}. $$
| $n$ | $W(n)$ |
|---|---|
| 1 | (1;0) |
| 10 | (1,0084;-0,022878) |
| 100 | (1,0084;-0,022881) |
| 1000 | (1,0084;-0,022881) |
| 10000 | (1,0084;-0,022881) |
| 100000 | (1,0084;-0,022881) |
| 1000000 | (1,0084;-0,022881) |
Les mathématiciennes et mathématiciens notent plutôt $\zeta(x+it)$ que $\zeta(x;t)$ et $x+it$ plutôt que $(x;t)$. Ainsi, $\zeta\left(5,2+i(-7,3)\right)$ est le couple de réels dont le développement décimal commence par $1,008+i(-0.022)$. Enfin, on peut montrer qu’il est possible (par une autre formule que celle donnée ci-dessus) de calculer $\zeta(x+it)$ pour tous les couples de réels $(x;t)$ sauf pour le couple $(1;0)$. La fonction $\zeta$ s’appelle la fonction zêta de Riemann. L’hypothèse de Riemann énonce que, si $x$ n’est pas un entier pair strictement négatif et si $\zeta(x+it)$ est le couple $(0;0)$ alors $x=\frac{1}{2}.$
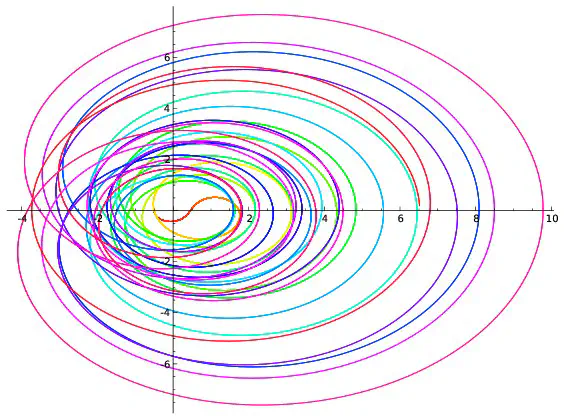
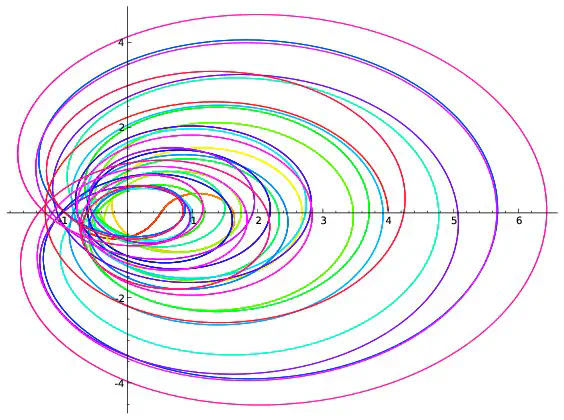
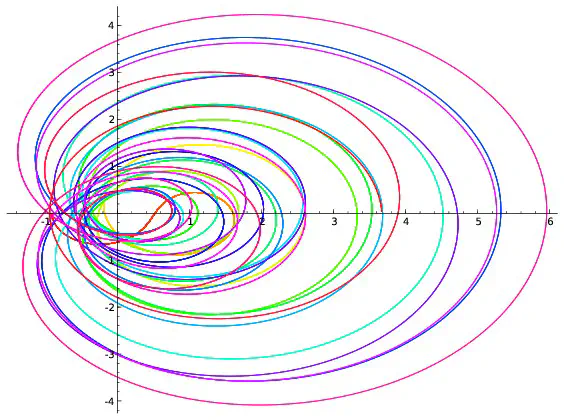
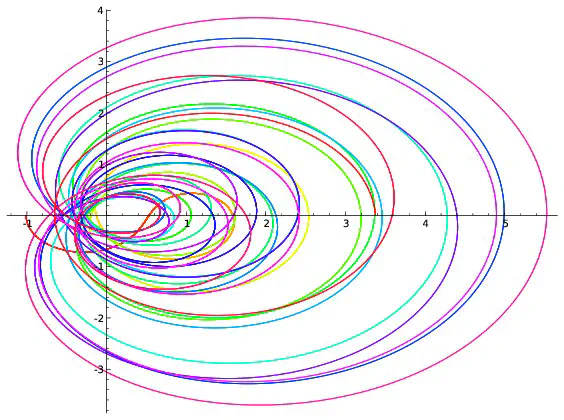
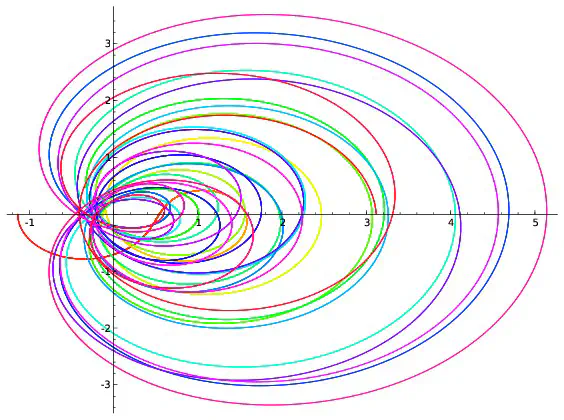
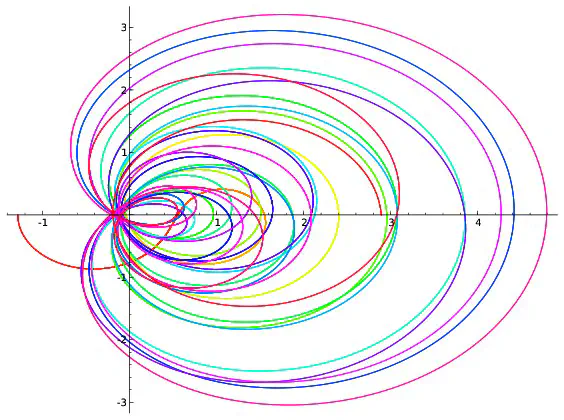
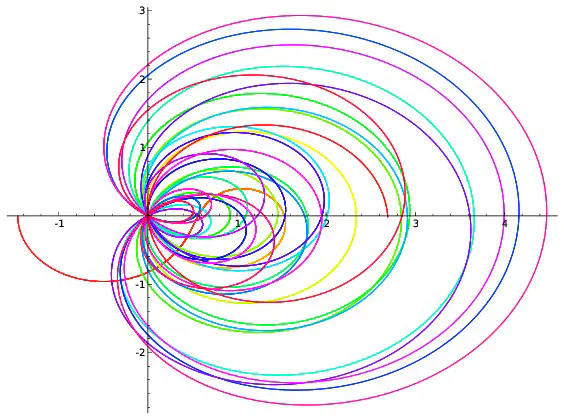
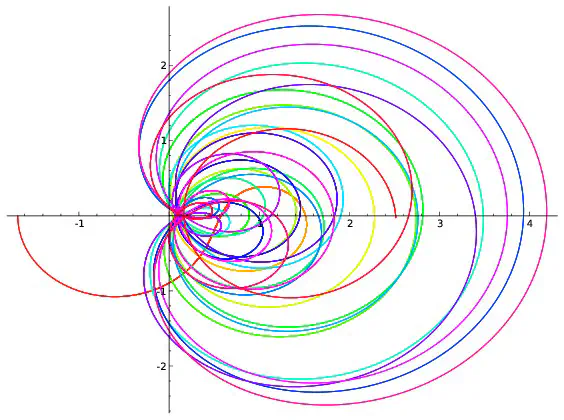
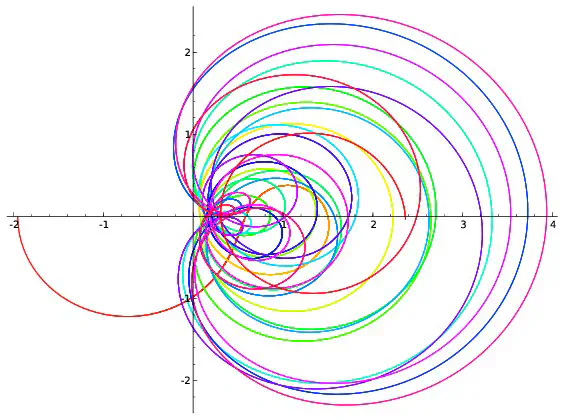
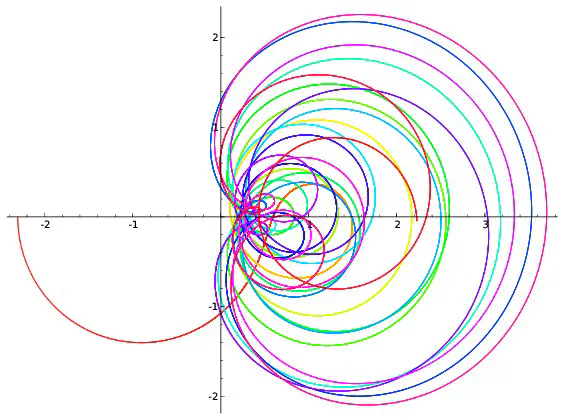
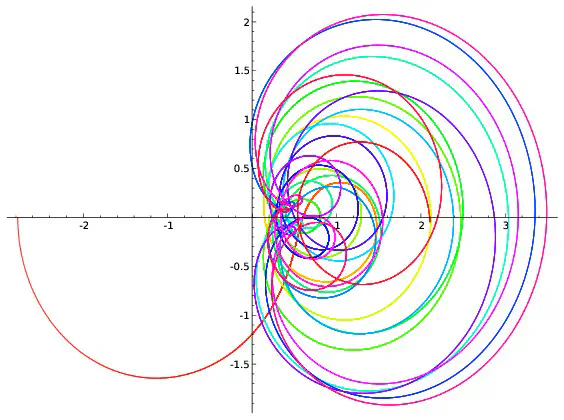
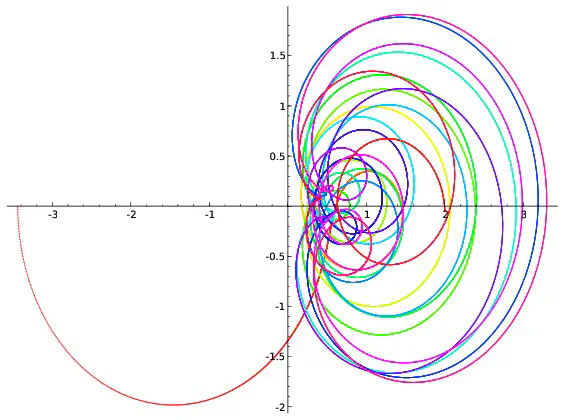
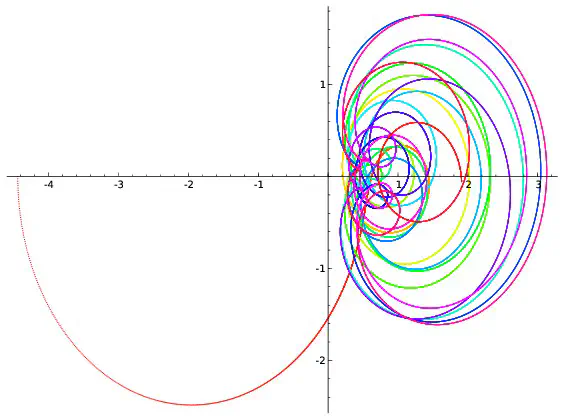
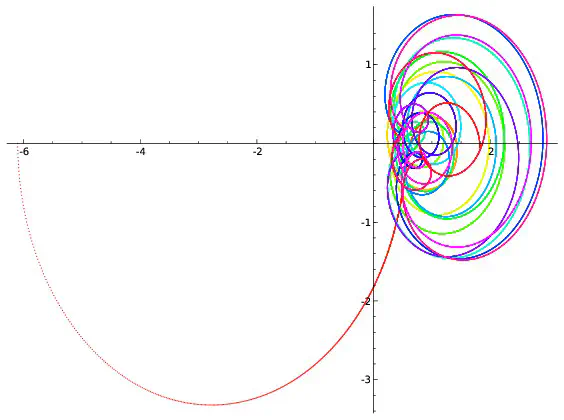
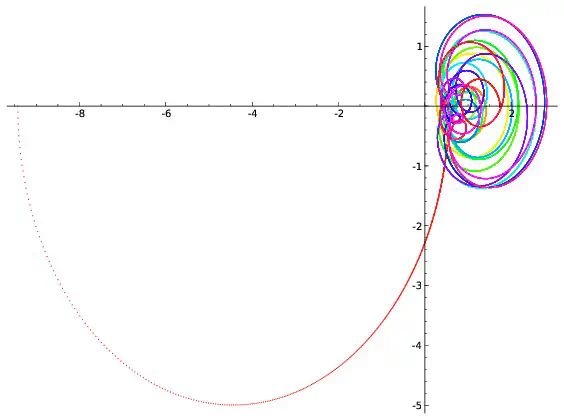
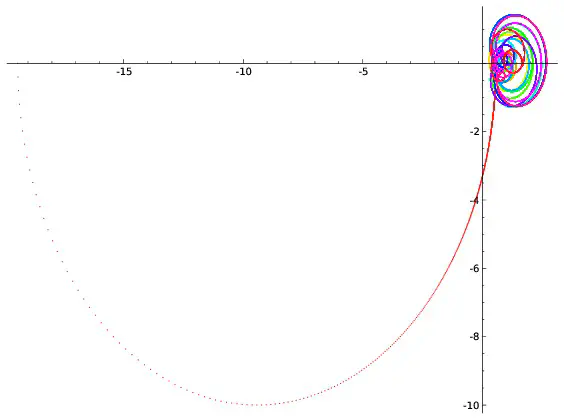
On peut visualiser l’hypothèse de Riemann à l’aide de dessins. On fixe un réel $x$, par exemple $x=0,2$. Pour chaque réel $t$, $\zeta(0,2+it)$ est un couple de réels que l’on représente en se repérant suivant deux axes, l’un horizontal, l’autre vertical. On peut par exemple montrer que $\zeta(0,2+i0,7)=-0,19+i(-0,56)$. Pour représenter ce point, on marque $-0,19$ sur l’axe horizontale et on trace une droite verticale passant par cette marque puis on repère $-0.56$ sur l’axe verticale et on trace une droite horizontale passant par cette deuxième marque. Le point représentant $-0,19+i(-0.56)$ est à l’intersection des droites horizontales et verticales qui viennent d’être tracées.
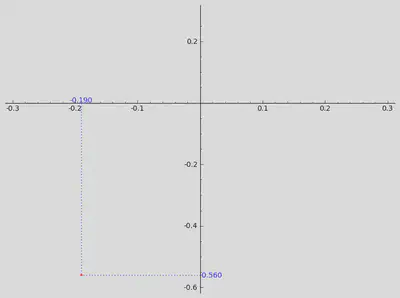
Afin de repérer aussi la valeur de $t$, on colorie le point suivant une couleur donnée par l’échelle ci-dessous.

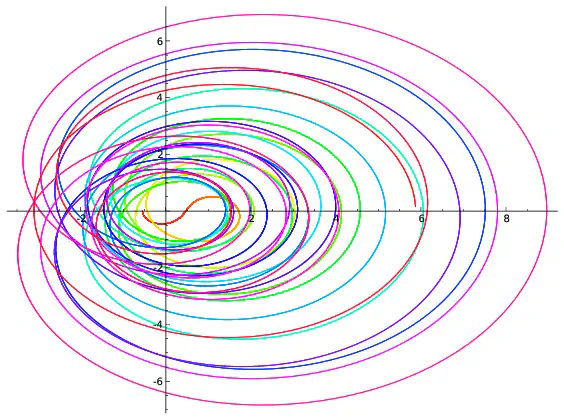
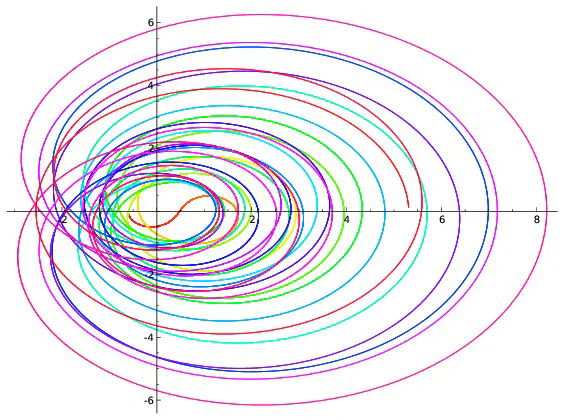
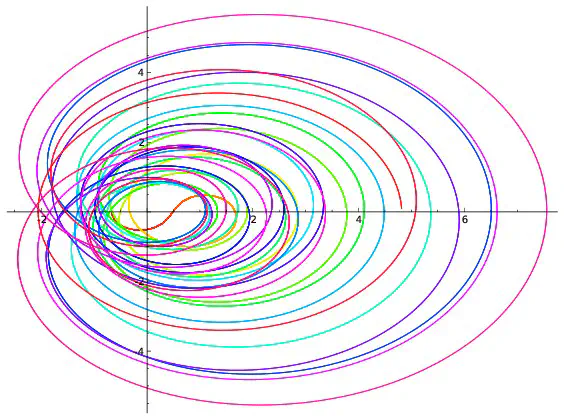
Si l’on répète ce procédé pour toutes les valeurs de $t$ comprises entre $0$ et $100$ et écartées de $0,001$, on obtient 100000 points qui forment une courbe. Ce sont ces courbes qui sont représentées ci-dessous pour différentes valeurs de $x$.
Parmi les courbes représentées, seule celle correspondant à $x=\frac{1}{2}$ passe par l’intersection des deux axes. Cela revient à dire que la seule valeur de $x$ pour laquelle existe au moins une valeur $t$ vérifiant $\zeta(x+it)=0+i0$ est $x=\frac{1}{2}$ ce qui est bien prédit par l’hypothèse de Riemann. Cependant les dessins ne démontrent rien : on ne voit pas ce qui se passe pour les valeurs de $x$ autres que celles représentées ; on ne voit rien pour les valeurs de $t$ supérieures à $100$. C’est dans l’étude de ce qui ne se voit pas que commencent les mathématiques… Les images précédentes correspondent à quelques valeurs de $x$. Construisons une image pour chaque valeur de $x$ comprises entre $0$ et $0,99$ avec des écarts de $0,01$. On obtient 100 images que l’on regroupe en un film disponible ci-dessous. On voit là encore (et on le voit mieux sur le deuxième film qui est un zoom du premier) que la seule courbe passant à l’intersection des axes est celle correspondant à $x=0,5$ ce qui est prédit par l’hypothèse de Riemann.
Pour écrire ce texte, je me suis inspiré des textes ou site suivants.
- Gérald Tenebaum & Michel Mendès France. Les Nombres premiers, entre l’ordre et le chaos. Dunod. 2011.
- Marcus Du Sautoy. La Symphonie des nombres premiers. Éloise d’Ormesson. 2003. (En poche : Points. 2007.)
- Le site de Jeffrey Stopple pour les images et le film (dans les films de Stopple, les couleurs représentent l’argument complexe).